Enforcing D2h during 2D PES_SCAN for cyclobutadiene

Questions
#1

Hello everyone,

Is there a way to constrain the point-group symmetry (D₂h) during a 2-D scan (JOBTYPE=PES_SCAN), so that opposite C–C bonds remain equal each other at every grid point?

CBD
CBD657×661 36.4 KB

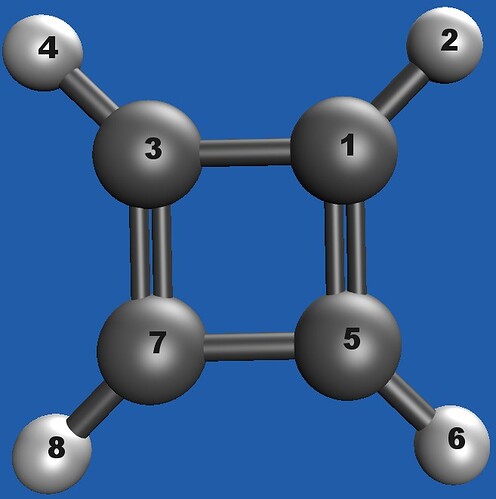
I’m scanning cyclobutadiene (CBD) with a symmetric Z-matrix. Opposite ring bonds are intended to stay equal: R(1–3) = R(5–7) and R(1–5) = R(3–7)

I run a 2-D frozen scan:

comment
 CBD CAS pes_scan 6-311++G(d,p)
$end

$molecule
0 1
C 
H  1 1.070965
C  1 R1        2 134.996727
H  3 1.070965  1 134.996727 2   -0.000000 0
C  1 R2        2 135.003273 3 -180.000000 0
H  5 1.070965  1 135.003273 2   -0.000000 0
C  5 R1        1  90.000000 2  180.000000 0
H  7 1.070965  5 134.996727 1  180.000000 0

R1=1.429784
R2=1.429784
$end

$rem
   JOBTYPE             = pes_scan    !Find transition state
   EXCHANGE hf
   UNRESTRICTED        = FALSE  ! For Closed-shell systems
    BASIS               = 6-311++G(d,p)
   SCF_CONVERGENCE     = 8
   POP_MULLIKEN        = FALSE 
   SYMMETRY            = TRUE 
   GEOM_OPT_MAX_CYCLES = 500
   sym_ignore          = FALSE   
   GUI                 = 2      
   mem_total           = 20000
   mem_static          = 8190
MAX_SCF_CYCLES 500
THRESH 12 
CAS_METHOD  2  
CAS_M_S     0  
CAS_N_ELEC  4  
CAS_N_ORB   4  
CAS_N_ROOTS 1  
CAS_THRESH 12  
MAX_CASSCF_CYCLES 500 
CAS_USE_RI FALSE 
CAS_DAVIDSON_TOL 5 
CAS_DAVIDSON_MAXVECTORS 10 
CAS_SOLVER 1 
TRUNC_CI_LEVEL 0 
ASCI_DIAG 2 
SCF_ALGORITHM diis_gdm 
FROZEN_SCAN TRUE
$end

$scan
stre   3     1   1.425       1.435  0.002
stre   5     1   1.425       1.435  0.002
$end

Q-Chem builds the full N×N grid (as expected), but the equality R(1–3)=R(5–7) is not maintained; e.g., As it is see in the attached distance matrix R(1–3)=1.435 while R(5–7) stays at its initial value (~1.429784).

                       Distance Matrix (Angstroms)
             C (  1)   H (  2)   C (  3)   H (  4)   C (  5)   H (  6)
   H (  2)  1.070965
   C (  3)  1.435000  2.319370
   H (  4)  2.319370  2.949487  1.070965
   C (  5)  1.435000  2.319424  2.029396  3.100361
   H (  6)  2.319424  2.949660  3.100361  4.171326  1.070965
   C (  7)  2.025712  3.096675  1.435009  2.321132  1.429784  2.314441
   H (  8)  3.096675  4.167640  2.317726  2.949664  2.314441  2.944271
             C (  7)
   H (  8)  1.070965

The question:
Can a 2-D PES_SCAN enforce either point-group symmetry*or equality constraints (e.g., R13=R57, R15=R37) at every grid point?
Thank you very much!

Q-Chem failing to recognize correct symmetry
#2

Does Q-Chem detect the point group symmetry? (What does it print out for the point group underneath the Cartesian coordinates in the SNO?) If not, then you need to build a symmetric structure. There’s a “symmetrize” command in IQmol that can help, and/or reduce the value of SYM_TOL in $rem to reduce the tolerance for detecting symmetry.

Assuming that Q-Chem recognizes the structure as symmetric, there was an issue with the new geometry optimizer (libopt3) for a while, which allowed it to break symmetry. This has been resolved in Q-Chem v. 6.3. For older versions, you can set GEOM_OPT_DRIVER = OPTIMIZE in $rem to use the old optimizer, which should preserve the initial point-group symmetry.