Because of its balance in computational accuracy and cost, TDDFT has become the most popular theoretical method for excited state calculations. It is almost a blackbox theory for non-experts, which requires only minimum inputs such as the no. of excited states and the choice of exchange-correlation functional. Hence TDDFT can be successfully used even by experimentalists. Q-Chem offers both simple settings for routine TDDFT calculations and flexible options to meet the special needs of advanced TDDFT users.
One big difficulty of calculating core excited states involved in core electron spectroscopy is that these core excited states are very high in energy, and there could be too many (could be more than thousands in large systems) valence and core excited states lying below them, so that in within the popular linear-response TDDFT formalism, using any common bottom-up algorithm to locate core excited states starting from the first valence excited state become very tedious. Q-Chem adopts the strategy of reduced excitation space(a.k.a. restricted excitation window, restricted channel or energy-specific TDDFT in the literature), which means only the excitations from the relevant core orbitals are considered in solving the TDDFT linear response equation. With this approach, computational costs of core excitations show no difference from those of valence excitations.
Another problem with TDDFT calculations of core excited states is that standard exchange–correlation functionals significantly underestimate core excitation energies. In Q-Chem, there are specially designed short-range corrected exchange-correlation functionals (the SRC functionals) available, which substantially improve the calculated core excitation energies. Therefore we recommend to use the SRC functionals for core electron spectroscopy simulations.
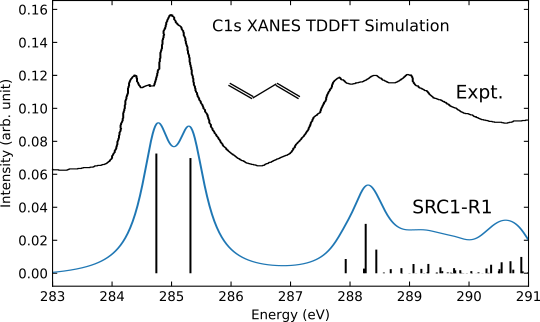
Here we present an example of TDDFT simulation of the C1s X-ray absorption spectrum of trans-1,3-butadiene using the short-range corrected exchange-correlation functional SRC1-R1. The geometry has been optimized at the MP2/cc-pVTZ level of theory.
Example. TDDFT simulation of the C1s X-ray absorption spectrum of trans-1,3-butadiene.
Q-Chem input and comments (after “!”):
$molecule
0 1
C 1.8416159364 -0.0902003508 0.0000000000
C 0.5989671377 0.4113680064 0.0000000000
H 0.4548909390 1.4862789272 0.0000000000
H 2.0075936225 -1.1592617432 0.0000000000
H 2.7088998342 0.5528424826 0.0000000000
C -0.5989671377 -0.4113680064 0.0000000000
H -0.4548909390 -1.4862789272 0.0000000000
C -1.8416159364 0.0902003508 0.0000000000
H -2.7088998342 -0.5528424826 0.0000000000
H -2.0075936225 1.1592617432 0.0000000000
$end
$rem
EXCHANGE SRC1-R1 ! the short-range corrected xc functional SRC1 for row1 elements
BASIS 6-311(2+,2+)G** ! large basis sets should be used to obtain reliable results
CIS_N_ROOTS 100 ! no. of excited states is determined by the spectral energy range
CIS_TRIPLETS false ! no triplet calculation for a closed shell system
TRNSS true ! invoke the reduced excitation space algorithm
TRTYPE 3 ! specify a set of occupied orbitals, no restriction on virtual orbitals
N_SOL 4 ! no. of occupied orbitals in the reduced excitation space
$end
$solute
1
2
3
4
$end
Note: The indices of the 4 occupied orbitals are listed in the $solute section. Here we want to calculate the C1s core excitations, therefore we put all C1s core orbitals (with the orbital indices 1-4) into the reduced excitation space. Warning: incomplete core excitation space (for example here, only list 1 or 1, 2 in the $solute section) would lead to erroneous results!
The simulated XAS signal is shown in the following figure: