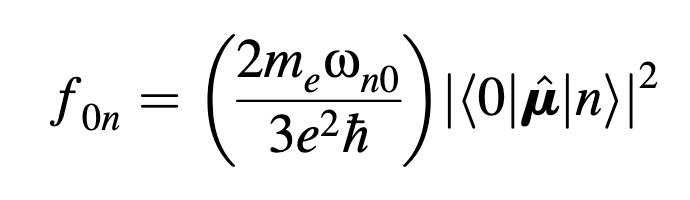Oscillator strength formula

[marand71]

Dear users and developers!
I am wondering what formula is used by Q-Chem to compute the oscillator strength in TDDFT.

Regardless of the constants, the oscillator strength (for absorption) should be proportional to the square of the transition dipole moment and to the energy of transition.

I have certain doubts concerning the values produced by QChem. I have calculated the the excitation energies and TDMs for the same transition in two different solvents:

For cyclohexane, the TDM is 1.13689D, the excitation energy is 3,688 eV, and the “strength” (produced in the section of the output is 0.11752)
For acetonitrile, the respective values are 1.29375D, 3.717eV, and 0.12381

First of all, the ratio of the quantity: mi^2*Energy in the two solvents (0,76609) is not equal to the ratio of the “strengths” (0,94922).

Secondly, the textbook formula for the oscillator strength f=1.08603e-5*v(in 1/cm)*mi(in atomic units)^2, with the calculated quantities put in (with the correct units) give the oscillator strengths equal to: 0.06463 and 0.08435 for cyclohexane and acetonitrile, respectively.

The oscillator strength defined by the above equation is related to the transition intensity by the following formula: f=4.32e-9*[molar extinction coefficient integrated over the whole absorption band in the domain of wavenumbers].

Perhaps the quantity returned by Q-Chem is just defined in a different way? But then, could someone give the fomula relating the “strength” to TDM and to the oscillator strength that is defined by the equations I have included above.

Thank you very much for assistance
Yours
Marcin Andrzejak

[kaushik]

The oscillator strength for all quantities in atomic units is given by

f = 2/3 * (Exci. E) * (mu_x^2 + mu_y^2 + mu_z^2)

Consider the following calculation:

$molecule
0 1
O
H 1 1.1
H 1 1.1 2 110.
$end

$rem
method b3lyp
basis sto-3g
cis_n_roots 2
$end

You can verify that the output file generates the oscillator strengths consistent with the above formula for the two singlets. For example, for singlet 1 (state 2),

f = 2/3 * (-75.01109051+75.30712899)*(0^2+0.0877^2+0^2) = 0.001518,

which is consistent with the printed value.

[jherbert]

From Redirecting
Should be

[marand71]

Exactly Thank you.