Simulating core photoelectron spectroscopy using the equation-of-motion coupled-cluster method for ionization potentials with the frozen-core and core-valence-separation approximations ((fc)-CVS-EOM-IP-CC)

yzhang · July 17, 2020, 5:41pm

X-ray lasers can trigger core ionization in a molecular system. The leaving electrons feel the electronic interaction in the molecular environment and thus carry the information of the electronic structure. Thanks to energy separation and locality of core ionizations, core photoelectron spectroscopy with X-ray has excellent element selectivity and spatial resolution, which makes it a powerful experimental tool in modern chemistry, physics, materials science and biology.

As correlation plays an important role in core ionization, high-level correlated methods such as coupled cluster (CC) theory are usually used to simulate core photoelectron spectroscopy (PES). CC and its equation-of-motion (EOM) variant are among the most accurate and versatile tools in studying core level spectroscopy. To consider ionizations, the EOM-IP-CC approach is adopted, in which the ground state is treated at the CC level and the ionized states are accessed by applying an ionization operator to the ground-state wavefunction. In order to reduce the computational cost, the CC calculations are done under the frozen core (fc) approximation, which means the ground state amplitudes and multipliers with occupied indices referring to a core orbital are set to zero and hence the core-core and core-valence correlation in the ground state is neglected. Since we only care about core ionizations here, the EOM states are represented in a restricted Fock space spanned by the many-electron determinants with at least one occupied core orbital index (the core-valence-separation approximation). The above sketches the main profile of the fc-CVS-EOM-CC approach.

Both ground states and excited state core PES can be studied by fc-CVS-EOM-CCSD. In ground state studies, the ionized states are obtained by fc-CVS-EOM-IP-CCSD, and the corresponding left- and right-Dyson orbitals are calculated, as the transformed Hamiltonian in the CC equations are not hermitian. The ionization intensities can be estimated using the product of norms of the left- and right-Dyson orbitals. The case of excited state core PES is different from that of ground states, since the final states of core ionization have double excitation character (2-hole-1-particle), which are not well described by at the level of EOM-CCSD. A scheme to circumvent this difficulty is to first obtain an excited triplet state with a valence hole through MOM, and then use this excited triplet state as a reference to calculate the core-ionized states and the corresponding left- and right-Dyson orbitals. Core ionizations from both alpha and beta channels show similar results.

In the following examples we show how to calculate the ground state PES of adenine and the excited state PES of uracil through fc-CVS-EOM-IP-CCSD.

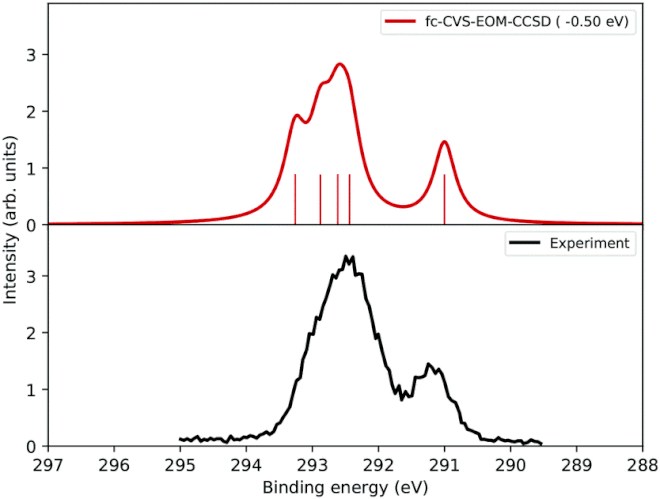
Example. Simulating the C1s PES of the ground state of adenine. Geometry optimized at the MP2/cc-pVTZ level of theory.

Q-Chem input and comments (after “!”. Comments outside of the $rem section should be removed in order to run the qchem calculation.):

$molecule
0 1
N       1.663948    -1.127531    0.000000
N      -0.643862    -1.804088    0.000000
N      -0.636159     1.773662    0.000000
N      -2.146840     0.119893    0.000000
N       2.353671     1.084678    0.000000
C       0.668787    -2.022720    0.000000
C      -0.919981    -0.499328    0.000000
C       0.000000     0.546991    0.000000
C       1.356490     0.175959    0.000000
C      -1.907009     1.474843    0.000000
H      -3.039931    -0.341646    0.000000
H      -2.712908     2.189994    0.000000
H       0.978346    -3.060960    0.000000
H       2.144452     2.065199    0.000000
H       3.305020     0.766647    0.000000
$end

$rem
print_general_basis = true
jobtype = sp
method = eom-ccsd
cvs_ip_states    [5,0]    ! calculate 5 ionized states in the first irrep, none for the second.
basis = general    ! a general 6-311(2+,+)G** basis set is used (uncontracted core on C)
n_frozen_core = fc    ! the frozen core approximation
cc_trans_prop = true    ! calculate the transition properties of CC states
cc_do_dyson = true    ! calculate Dyson orbitals
print_general_basis = true
molden_format = true    ! output the orbitals in the MOLDEN format
$end

$basis
H    0
6-311(2+,+)G**
****
O    0
6-311(2+,+)G**
****
N    0
6-311(2+,+)G**
****
C    0
S    1    1.000000
   4.56324000E+03    1.00000000E+00    ! uncontracted core on C
S    1    1.000000
   6.82024000E+02    1.00000000E+00
S    1    1.000000
   1.54973000E+02    1.00000000E+00
S    1    1.000000
   4.44553000E+01    1.00000000E+00
S    1    1.000000
   1.30290000E+01    1.00000000E+00
S    1    1.000000
   1.82773000E+00    1.00000000E+00
SP   3    1.000000
   2.09642000E+01    1.14660000E-01   4.02487000E-02
   4.80331000E+00    9.19999000E-01   2.37594000E-01
   1.45933000E+00   -3.03068000E-03   8.15854000E-01
SP   1    1.000000
   4.83456000E-01    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   1.45585000E-01    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   4.38000000E-02    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   1.31927711E-02    1.00000000E+00   1.00000000E+00
D    1    1.000000
   6.26000000E-01    1.00000000E+00
****
$end

The simulation results are shown in the following figure:

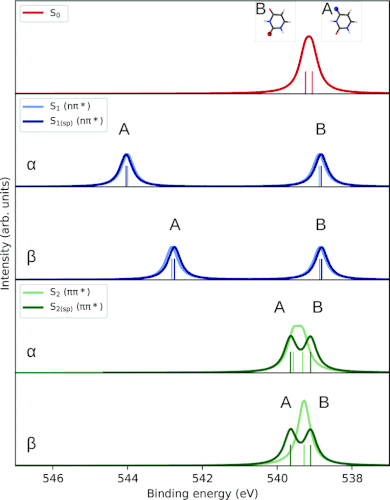
Example. Simulating the O1s PES of the excited state (S1) of uracil. Geometry optimized at the CCSD/aug-cc-pVDZ level of theory.

Q-Chem input and comments (after “!” in. Comments outside of the $rem section should be removed in order to run the qchem calculation.):

$comment
First step: a HF single point calculation of the neutral singlet state
$end

$molecule
0 1
C        -0.0042112405          -1.7549930536        0.0000000000
H        -2.0949460216          -1.4184138214        0.0000000000
H        -0.1300971688          -2.8358204634        0.0000000000
H          0.0374086733    2.0243048927        0.0000000000
C        -1.2210197500    0.4010705948        0.0000000000
O        -2.2535781024    1.0567627444        0.0000000000
C          1.2399442445    0.2839850904        0.0000000000
O          2.3361887279    1.0691923037        0.0000000000
N          0.0349480223    1.0125648826        0.0000000000
N        -1.1853832587          -0.9770870742        0.0000000000
C          1.2251302704          -1.1165150648        0.0000000000
H          2.1596039787          -1.6767971209        0.0000000000
$end

$rem
jobtype sp
basis general
method hf
n_frozen_core = 2    ! freeze 2 O1s electrons
$end

$basis
H    0
6-311(2+,+)G**
****
O    0
S    1    1.000000
   8.58850000E+03    1.00000000E+00
S    1    1.000000
   1.29723000E+03    1.00000000E+00
S    1    1.000000
   2.99296000E+02    1.00000000E+00
S    1    1.000000
   8.73771000E+01    1.00000000E+00
S    1    1.000000
   2.56789000E+01    1.00000000E+00
S    1    1.000000
   3.74004000E+00    1.00000000E+00
SP   3    1.000000
   4.21175000E+01    1.13889000E-01   3.65114000E-02
   9.62837000E+00    9.20811000E-01   2.37153000E-01
   2.85332000E+00   -3.27447000E-03   8.19702000E-01
SP   1    1.000000
   9.05661000E-01    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   2.55611000E-01    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   8.45000000E-02    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   2.54518072E-02    1.00000000E+00   1.00000000E+00
D    1    1.000000
   1.29200000E+00    1.00000000E+00
****
N    0
S    1    1.000000
   6.29348000E+03    1.00000000E+00
S    1    1.000000
   9.49044000E+02    1.00000000E+00
S    1    1.000000
   2.18776000E+02    1.00000000E+00
S    1    1.000000
   6.36916000E+01    1.00000000E+00
S    1    1.000000
   1.88282000E+01    1.00000000E+00
S    1    1.000000
   2.72023000E+00    1.00000000E+00
SP   3    1.000000
   3.06331000E+01    1.11906000E-01   3.83119000E-02
   7.02614000E+00    9.21666000E-01   2.37403000E-01
   2.11205000E+00   -2.56919000E-03   8.17592000E-01
SP   1    1.000000
   6.84009000E-01    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   2.00878000E-01    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   6.39000000E-02    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   1.92469880E-02    1.00000000E+00   1.00000000E+00
D    1    1.000000
   9.13000000E-01    1.00000000E+00
****
C    0
S    1    1.000000
   4.56324000E+03    1.00000000E+00
S    1    1.000000
   6.82024000E+02    1.00000000E+00
S    1    1.000000
   1.54973000E+02    1.00000000E+00
S    1    1.000000
   4.44553000E+01    1.00000000E+00
S    1    1.000000
   1.30290000E+01    1.00000000E+00
S    1    1.000000
   1.82773000E+00    1.00000000E+00
SP   3    1.000000
   2.09642000E+01    1.14660000E-01   4.02487000E-02
   4.80331000E+00    9.19999000E-01   2.37594000E-01
   1.45933000E+00   -3.03068000E-03   8.15854000E-01
SP   1    1.000000
   4.83456000E-01    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   1.45585000E-01    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   4.38000000E-02    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   1.31927711E-02    1.00000000E+00   1.00000000E+00
D    1    1.000000
   6.26000000E-01    1.00000000E+00
****
$end

@@@

$comment
Second step: read in the MOs from the previous step, and obtain a neutral triplet excited state through MOM, then run CVS-EOM-IP-CCSD to calculate the ionized states
$end

$molecule
0 3    ! triplet  configuration is considered as reference for core ionization
C        -0.0042112405       -1.7549930536    0.0000000000
H        -2.0949460216       -1.4184138214    0.0000000000
H        -0.1300971688       -2.8358204634    0.0000000000
H         0.0374086733        2.0243048927    0.0000000000
C        -1.2210197500        0.4010705948    0.0000000000
O        -2.2535781024       1.0567627444     0.0000000000
C         1.2399442445        0.2839850904    0.0000000000
O         2.3361887279       1.0691923037     0.0000000000
N         0.0349480223       1.0125648826     0.0000000000
N       -1.1853832587       -0.9770870742     0.0000000000
C        1.2251302704       -1.1165150648    0.0000000000
H        2.1596039787       -1.6767971209    0.0000000000
$end

$rem
job_type  =  sp
basis  = general
print_general_basis = true
method  =  eom-ccsd
Scf_guess = read    ! read in the MOs from the previous step 
mom_start = 1        ! invoke MOM to obtain an excited state
cvs_ip_states = [4,0]    ! calculate 4 ionized states in the first irrep, none for the second.
cvs_eom_shift = 19500    ! specifies energy shift in CVS-EOM calculations.
n_frozen_core = 2    ! freeze 2 O1s electrons
cc_trans_prop = true    ! calculate the transition properties of CC states
cc_do_dyson = true    ! calculate Dyson orbitals
molden_format = true    ! output the orbitals in the MOLDEN format
$end

$basis
H    0
6-311(2+,+)G**
****
O    0
S    1    1.000000
   8.58850000E+03    1.00000000E+00
S    1    1.000000
   1.29723000E+03    1.00000000E+00
S    1    1.000000
   2.99296000E+02    1.00000000E+00
S    1    1.000000
   8.73771000E+01    1.00000000E+00
S    1    1.000000
   2.56789000E+01    1.00000000E+00
S    1    1.000000
   3.74004000E+00    1.00000000E+00
SP   3    1.000000
   4.21175000E+01    1.13889000E-01   3.65114000E-02
   9.62837000E+00    9.20811000E-01   2.37153000E-01
   2.85332000E+00   -3.27447000E-03   8.19702000E-01
SP   1    1.000000
   9.05661000E-01    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   2.55611000E-01    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   8.45000000E-02    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   2.54518072E-02    1.00000000E+00   1.00000000E+00
D    1    1.000000
   1.29200000E+00    1.00000000E+00
****
N    0
S    1    1.000000
   6.29348000E+03    1.00000000E+00
S    1    1.000000
   9.49044000E+02    1.00000000E+00
S    1    1.000000
   2.18776000E+02    1.00000000E+00
S    1    1.000000
   6.36916000E+01    1.00000000E+00
S    1    1.000000
   1.88282000E+01    1.00000000E+00
S    1    1.000000
   2.72023000E+00    1.00000000E+00
SP   3    1.000000
   3.06331000E+01    1.11906000E-01   3.83119000E-02
   7.02614000E+00    9.21666000E-01   2.37403000E-01
   2.11205000E+00   -2.56919000E-03   8.17592000E-01
SP   1    1.000000
   6.84009000E-01    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   2.00878000E-01    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   6.39000000E-02    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   1.92469880E-02    1.00000000E+00   1.00000000E+00
D    1    1.000000
   9.13000000E-01    1.00000000E+00
****
C    0
S    1    1.000000
   4.56324000E+03    1.00000000E+00
S    1    1.000000
   6.82024000E+02    1.00000000E+00
S    1    1.000000
   1.54973000E+02    1.00000000E+00
S    1    1.000000
   4.44553000E+01    1.00000000E+00
S    1    1.000000
   1.30290000E+01    1.00000000E+00
S    1    1.000000
   1.82773000E+00    1.00000000E+00
SP   3    1.000000
   2.09642000E+01    1.14660000E-01   4.02487000E-02
   4.80331000E+00    9.19999000E-01   2.37594000E-01
   1.45933000E+00   -3.03068000E-03   8.15854000E-01
SP   1    1.000000
   4.83456000E-01    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   1.45585000E-01    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   4.38000000E-02    1.00000000E+00   1.00000000E+00
SP   1    1.000000
   1.31927711E-02    1.00000000E+00   1.00000000E+00
D    1    1.000000
   6.26000000E-01    1.00000000E+00
****
$end

$occupied    ! specify the orbital occupation
1:29 41    ! alpha orbitals no. 1-29 and 41 are occupied, which is specific to state S1
1:26 28 29    ! beta orbital no. 1-29 are occupied except no. 27, which is specific to state S1
$end

The simulation results are shown in the following figure:

yzhang · July 27, 2020, 6:17am

This howto is prepared with the help from Marta Lopez Vidal at Technical University of Denmark.

KMZ · February 25, 2021, 8:43pm

Dear yzhang,

thank you for this very interesting tutorial.
May I ask you two questions:

What is the difference to the fc-CVS-EOM-EE-CC approach presented in the manual and in Webinar 36?
I understood that the number of frozen core is very important and edge sensitive. How does one account for this if there are (as it is in your case) several degenerate core orbitals. Are by choosing n_frozen_core = fc all C core orbitals included ?

Best
Michael

yzhang · February 26, 2021, 12:03am

Dear Michael,
My answers to your questions are as the following:

I think the fc-CVS-EOM-EE/IP-CC approach were covered in webinar 36. As I presented in the introduction section of the tutorial above, the frozen core (fc) approximation means the ground state amplitudes and multipliers with occupied indices referring to a core orbital are set to zero and hence the core-core and core-valence correlation in the ground state is neglected. And in the core-valence-separation approximation the EOM states are represented in a restricted Fock space spanned by the many-electron determinants with at least one occupied core orbital index.
Yes, all C1s core orbitals are frozen is you set n_frozen_core = fc.

KMZ · February 26, 2021, 9:19am

Dear yzhang,

thank you for your prompt reply.
I am sorry I think I did not express myself very clear. I meant what is the difference in calculation ground state XAS via the EOM-EE or EOM-IP approach. Why should one choose one or the other. In the webinar they only showed the calculation of ground state XAS via EOM-EE and so does the manual 5.1. Thus, I am very interested in this new way of calculating XAS with the EOM-IP version you outlined above. Do you expect differences with the two approaches? Or are there computational cost benefits?
Regarding my second question, I understand that all C1s orbitals are frozen and also all N1s orbitals I assume. So overal 6 x 1s orbitals. My question is now which 1s - valence transition are included if I set n_frozen_core = fc. According to the manual it is edge sensitive and only the highest lying frozen orbital is incorporated. So in case I wanted the nitrogen edge, I would need to unfreeze the C1s orbitals. In your example we have several Carbon 1s orbitals. They will not all have the same orbital energy, since their chemical environment is different. So by freezing all 1s orbitals, and since only the 1s orbital highest in energy is regarded for the transition, I was just wondering if you still include XAS transitions from all 4 Carbon atoms or only from the one with the 1s highest in energy?

Thank you very much,
Michael

yzhang · February 26, 2021, 6:09pm

hi, Michael,
I think in webinar 36 it was stated that CVS-EOM-IP is for XPS and XES, while CVS-EOM-EE is for XAS and RIXS. In the tutorial above I was talking about XPS, so I used CVS-EOM-IP.
For your second question, I will talk to the original author of the code and get back to you.
Thanks
Yu

yzhang · March 1, 2021, 7:57am

I have consulted the author of the code and get the following answer to your second question: you will get transitions from all 4 carbon atoms if you do not ask for too less ionized states in your calculation (for example, only 1 or 2 ionized states).

AnnaKrylov · March 2, 2021, 5:36pm

The difference between using EOM-IP and EOM-EE is the type of the target states you are accessing. For example, if you want to compute core and valence ionization energies and XES transitions in benzene molecule, you will need to use EOM-IP and CVS-EOM-IP with a closed-shell neutral reference. If you would like to compute XAS and RIXS of the neutral benzene, then you need to use EOM-EE and fc-EOM-EE, again, with the neutral reference. In all cases, you should use FC=6 to freeze all 6 core orbitals (which is the default setting for both calculations).

You may find this review paper useful:
http://arjournals.annualreviews.org/eprint/ukNyyVKWir2agwdJ5RPx/full/10.1146/annurev.physchem.59.032607.093602

It explains the EOM-CC approach approach and gives examples.

AnnaKrylov · March 2, 2021, 5:40pm

And as a general introduction to the EOM-CC methods in Q-Chem, you can watch this webinar:
https://www.q-chem.com/webinars/3/

KMZ · June 10, 2021, 9:40pm

Dear @AnnaKrylov and @yzhang ,
thank you very much for your detailed answers. The last months I did some calculations with TRNSS-TDDFT und EOM-CC to calculate electronic ground state XAS. Most of the time the two methods give nearly the same results (apart from a different absolute shift). At least after I moved to QChem 5.3. Using the older 5.1 version did not converge cvs-EOM-CC simulations.
I was now moving to XAS with excited electronic reference (TR-XANES) and reading up on it in this paper https://aip.scitation.org/doi/10.1063/1.5115154. I am a bit stuck by how I should ideally construct my electronic excited state reference. I understand based on the paper (page 151) and on the text above for XPS, that to overcome convergence problems, one should use high-spin open-shell reference with the same character as the desired electronic excited reference. This raises a bit a understanding issue. My target reference state is a singlet state and so are my final TR-XAS states. Do I not calculate the wrong properties by just putting it all in triplet states? I now have alpha and beta core orbital excitations of the same character but different excitation energies. And – in my eyes – no clear indication which one to use for my actual singlet TR-XAS. But maybe I am getting something wrong here? I also – sadly – do not get a core - SOMO transition with the triplet reference.
This might be because I understand the paper referenced above wrong? After explaining the usage of the tripet reference on page 151 the authors use in the following analysis singlet references (e.g. Fig 14/15) to calculate the SOMO transition. So should I use singlet excited electronic references and not triplet? I am a bit confused by this point. It might have to do with the discussion about the ‘shake-up’ in the paper and the analogous excitation patterns that arises from conventional ground-state reference, but I have to admit this paragraph is not entirely clear to me. Are you using no excited references at all in the end and calculate everything from the ground state?
These are quite some detailed questions. I hope I could make myself clear and I would very much appreciate and welcome any hints or tips here. I think these are really powerful methods in Qchem, I just have to figure out their final correct usage.
Thanks a lot in advance

yzhang · June 15, 2021, 11:53pm

I haven’t run such calculations before but am trying to understand the reference issue as the following: look at Fig. 11 in the paper you addressed, you will see a high-spin open-shell reference state with a valence hole (in orbital 6ag) and the core excited final state. The discussion above Fig. 11 simply tells you that if you choose the Ms = 0 MOM state (not a spin-pure state!) as the reference, CCSD calculations often have convergence issues. While if you start from the high-spin open-shell reference state (triplet), and excite the appropriate core electron (in Fig. 11, it is the beta electron) to the valence hole (core to SOMO transition), you will reach the final core excited state (triplet) without CCSD convergence issue. Here your target core excited state is a triplet but what you care about are the core excitation energies and transition dipoles, and those calculated quantities are demonstrated good in the paper.
Hope this can help.

KMZ · June 16, 2021, 8:24pm

Thanks for your reply.
I understand that by this scheme the SOMO transition might still be well represented. But what about other core excitation apart from the SOMO? With an excited reference state I will get other excitations from the core orbitals to valence orbitals, that are not the SOMO. And for these I suddenly have two options and two results. One from the alpha core and one from the beta core orbital. And in my case they differ quite substantially in energy due to the fact that the SOMO orbital will destabilse one of the two spin states and the resulting transition to a non-SOMO valence state.

yzhang · June 17, 2021, 4:19pm

I’m trying to contact the original authors of the paper and hope they can give you a detailed answer.