Understanding the vibrational fine structure of electronic absorption and emission (vibronic) and vibrational resonance Raman spectroscopy plays an important role in characterizing molecular and electronic structure of molecules. In principle one needs the information of vibrational states on top of different electronic states to determine the corresponding spectroscopy signals.
Q-Chem provides a module VIBRONIC implemented by Xunkun Huang, Huili Ma and Wanzhen Liang [1-3] to simulate vibrationally resolved one-photon absorption (OPA) and one-photon emission (OPE) as well as resonance Raman spectroscopy (RRS). The key quantity to determine OPA, OPE and RRS signals is the polarizability tensor, which is usually in the form of sum-over-states (SOS). Evaluating SOS expressions could make the simulation costly. In the VIBRONIC module, the SOS expression is transformed into the time domain and the polarizability tensor is calculated through Fourier transform of the Green’s function (propagator) in the time domain. Currently the VIBRONIC module is available in TDHF, CIS and TDDFT calculations.
Since for these spectroscopies (OPA, OPE and RRS), two electronic states (the ground state g and the excited state e) are involved, the signal simulation usually consists of two steps (one step for each electronic state) except in the VG model. Available theoretical models at different levels of approximation include:
- FC1 (available for OPA, OPE and RRS simulation). The Franck-Condon (FC) approximation is employed. In this model both ground and excited state geometries are required, but on the ground state vibrational frequencies are necessary. The excited state vibrational frequencies are assumed the same as the ground state vibrational frequencies and the Duschinsky rotation effect is neglected.
- FC2 (available for OPA, OPE and RRS simulation). The Franck-Condon approximation is employed. Optimized geometries and vibrational frequencies are required both for the ground and excited states. Duschinsky rotation is included.
- FCHT (available for OPA, OPE and RRS simulation). Both the FC and Hertzberg-Teller (HT) terms in the transition dipole moment Taylor expansion are considered. Optimized geometries and vibrational frequencies are required both for the ground and excited states. Duschinsky rotation is included.
- VG (available for OPA and RRS simulation). The vertical gradient (VG) approximation is employed. Only ground state optimized geometry and vibrational frequencies are required and so the simulation can be finished in one step. The excited state vibrational frequencies are assumed the same as the ground state vibrational frequencies and the Duschinsky rotation effect is neglected. The displacement vector between the ground and excited state vibrational normal modes are approximately calculated from the excited state energy gradients (available in excited state force calculations). HT terms are also neglected.
The following are examples of vibronic spectroscopy and RRS simulations. Please make sure both steps of calculations should access the same scratch directory, as the vibronic parameters saved from the previous step should be available for the later step. In order to do so, one can either run a two-step job using the “@@@” delimiter, or run two separated calculations with the same predefined scratch directory name. For example, running the following commands:
qchem input_file_for_state_1 output_file_for_state_1 your_scratch_directory_name
qchem input_file_for_state_2 output_file_for_state_2 your_scratch_directory_name
The vibronic spectra simulation must run after the vibronic parameters are saved (see the examples below). In all simulations the $rem variable SYM_IGNORE must be set to TRUE in order to prevent the molecular geometry being transformed to the standard orientation. Q-Chem provides two $rem variables and one input section to control vibronic spectra simulation. For details please refer to the manual.
Example 1. Simulating the OPA signals of formaldehyde with TDDFT and the FC1 model.
Q-Chem Input for step 1: excited state (S1) geometry optimization (comments are put after the “!” sign and should be removed in case qchem does not run properly)
$molecule
0 1
O 0.003000000 0.00000000 0.68241638
C 0.020000000 0.00000000 -0.57598362
H -0.030000000 0.92664718 -1.11098362
H 0.004000000 -0.92664718 -1.11098362
$end
$rem
jobtype opt
method b3lyp
basis def2-TZVP
cis_state_deriv 1 ! excited state no. 1
cis_singlets true
cis_triplets false
cis_n_roots 10
sym_ignore true ! this must be set to TRUE
save_vibronic_params true ! save the vibronic parameter for later use
$end
Q-Chem Input for step 2: ground state (S0) geometry optimization and frequency and OPA simulation (comments are put after the “!” sign and should be removed in case qchem does not run properly)
$molecule
0 1
O 0.00000000 0.00000000 0.68241638
C 0.00000000 0.00000000 -0.57598362
H -0.00000000 0.92664718 -1.11098362
H 0.00000000 -0.92664718 -1.11098362
$end
$rem
jobtype opt
method b3lyp
basis def2-TZVP
sym_ignore true
$end
@@@
$molecule
read
$end
$rem
jobtype freq
method b3lyp
basis def2-TZVP
sym_ignore true
vibronic_spectra 1 ! simulating OPA
$end
$vibronic ! the input section to control vibronic spectra simulation
model 1 ! using the FC model
freq_range 20000. 60000. 10. ! simulation frequency range parameters in cm-1.
time_range 1.0000000 40000 ! time step size in a. u. and no. of steps.
damping 40.00000 ! damping factor in cm-1.
$end
Note: in order to break the symmetry, the starting geometry in step 1 is slightly different from that in step 2. In addition, excited state geometry optimization could be subtle. One should make sure the target excited state does not change its character (e. g., the order of all calculated excited states has not changed) during the geometry optimization process.
The resulted OPA signals are saved in a file named “abs_spectra.dat” and can be plotted as
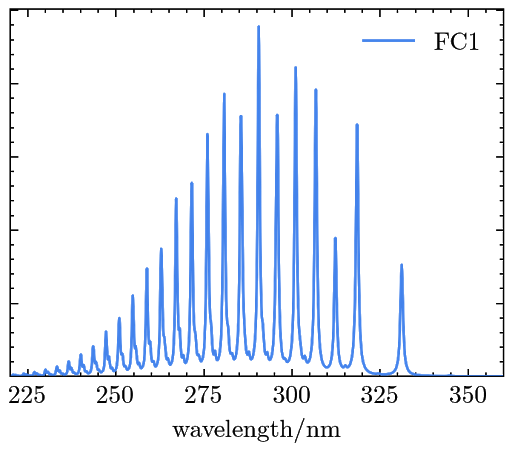
The scratch files used in the OPA signal calculation can be found in a directory called “your_output_file_name.files” under the same directory as where the output file is generated.
Example 2. Simulating the OPE signals of formaldehyde with TDDFT and the FC2 model.
Q-Chem Input for step 1: excited state (D1) geometry optimization and frequency calculation (comments are put after the “!” sign and should be removed in case qchem does not run properly)
$molecule
0 2
C 1.4840482200 0.0000338155 0.0000000000
C 0.7160497031 0.0000524901 -1.2119311870
C -0.7159596058 0.0000542629 -1.2126930961
C -1.4043236629 0.0000543088 0.0000000000
C -0.7159596058 0.0000542629 1.2126930961
C 0.7160497031 0.0000524901 1.2119311870
C 2.8748450131 0.0000120580 0.0000000000
H 1.2370230923 0.0000896598 -2.1693859212
H -1.2717579173 0.0000412967 -2.1497435961
H -1.2717579173 0.0000412967 2.1497435961
H 1.2370230923 0.0000896598 2.1693859212
H 3.4346492051 0.0000003003 -0.9330758768
H 3.4346492051 0.0000003003 0.9330758768
F -2.7508602624 0.0000394216 0.0000000000
$end
$rem
jobtype opt
method b3lyp
basis def2-SVP
cis_state_deriv 1
cis_singlets true
cis_triplets false
cis_n_roots 10
sym_ignore true
$end
@@@
$molecule
read
$end
$rem
jobtype freq
method b3lyp
basis def2-SVP
cis_state_deriv 1
cis_singlets true
cis_triplets false
cis_n_roots 10
sym_ignore true
save_vibronic_params true ! save the vibronic parameter for later use
$end
Q-Chem Input for step 2: ground state (D0) geometry optimization and frequency calculation and OPE simulation (comments are put after the “!” sign and should be removed in case qchem does not run properly)
$molecule
0 2
C 1.4566183503 0.0129101640 0.0000000000
C 0.7101644786 0.0081907583 -1.2185833193
C -0.6759989496 -0.0007979055 -1.2214548662
C -1.3520058015 -0.0052290244 0.0000000000
C -0.6759989496 -0.0007979055 1.2214548662
C 0.7101644786 0.0081907583 1.2185833193
C 2.8635151754 0.0218512897 0.0000000000
H 1.2491028005 0.0118050196 -2.1666316459
H -1.2458865325 -0.0044564748 -2.1504521674
H -1.2458865325 -0.0044564748 2.1504521674
H 1.2491028005 0.0118050196 2.1666316459
H 3.4244334505 0.0256959046 -0.9338584025
H 3.4244334505 0.0256959046 0.9338584025
F -2.7015919823 -0.0141481171 0.0000000000
$end
$rem
jobtype opt
method b3lyp
basis def2-SVP
sym_ignore true
$end
@@@
$molecule
read
$end
$rem
jobtype freq
method b3lyp
basis def2-SVP
sym_ignore true
vibronic_spectra 2 ! simulating OPE
$end
$vibronic
model 1 ! using the FC model
temperature 0. ! simulation temperature in K.
freq_range 1. 40000. 10.
time_range 1. 40000
damping 20.
$end
Note: One should confirm that the excited state geometry really is at a local minimum by the calculated vibrational frequencies.
The resulted OPE signals are saved in a file named “emiss_spectra.dat” and can be plotted as
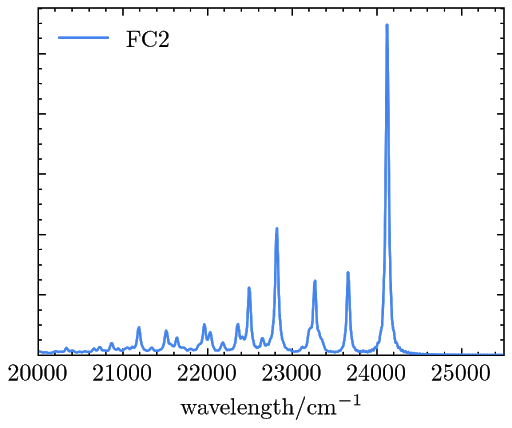
Example 3. Simulating the RRS signals of phenoxyl with TDDFT and the FCHT model.
Q-Chem Input for step 1: excited state (D3) geometry optimization and frequency calculation (comments are put after the “!” sign and should be removed in case qchem does not run properly)
$molecule
0 2
C 0.0000000000 1.2502862746 -1.0797670264
C 0.0000000000 0.0002405852 -1.8221303158
C 0.0000000000 -1.2495301785 -1.0796765524
C 0.0000000000 -1.2430453219 0.2902274202
C 0.0000000000 -0.0000629947 1.0386563677
C 0.0000000000 1.2431472440 0.2901098645
H 0.0000000000 2.1927860816 -1.6322129361
H 0.0000000000 -0.0006440427 -2.9122962915
H 0.0000000000 -2.1925083031 -1.6316088409
H 0.0000000000 -2.1692045915 0.8680624075
H 0.0000000000 2.1689368505 0.8682996003
O 0.0000000000 -0.0004016035 2.3373913028
$end
$rem
jobtype opt
method b3lyp
basis def2-SVP
cis_state_deriv 3 ! excited state no. 3
cis_singlets true
cis_triplets false
cis_n_roots 10
sym_ignore true
$end
@@@
$molecule
read
$end
$rem
jobtype freq
method b3lyp
basis def2-SVP
cis_state_deriv 3
cis_singlets true
cis_triplets false
cis_n_roots 10
sym_ignore true
save_vibronic_params true ! save the vibronic parameter for later use
$end
Q-Chem Input for step 2: ground state (D0) geometry optimization and frequency calculation and RRS simulation (comments are put after the “!” sign and should be removed in case qchem does not run properly)
$molecule
0 2
C 0.0000000000 1.2267763413 -1.0873977233
C 0.0000000000 0.0003129951 -1.7857718635
C 0.0000000000 -1.2259217607 -1.0872681918
C 0.0000000000 -1.2399944954 0.2921692642
C 0.0000000000 -0.0001222804 1.0534497246
C 0.0000000000 1.2400986319 0.2919975911
H 0.0000000000 2.1644176592 -1.6487443117
H 0.0000000000 -0.0006702414 -2.8784475224
H 0.0000000000 -2.1641202680 -1.6480392688
H 0.0000000000 -2.1702849650 0.8642269804
H 0.0000000000 2.1700059139 0.8643911139
O 0.0000000000 -0.0004975303 2.3044892072
$end
$rem
jobtype opt
method b3lyp
basis def2-SVP
sym_ignore true
$end
@@@
$molecule
read
$end
$rem
jobtype freq
method b3lyp
basis def2-SVP
sym_ignore true
vibronic_spectra 3 ! simulating RRS
$end
$vibronic
model 2 ! using the FCHT model
temperature 0.
freq_range 1. 4000. 1.
time_range 1. 40000
damping 100.
epsilon 25. ! line broadening factor for RRS, in cm-1.
$end
The resulted RRS signals are saved in a file named “rrs_spectra.dat” and can be plotted as
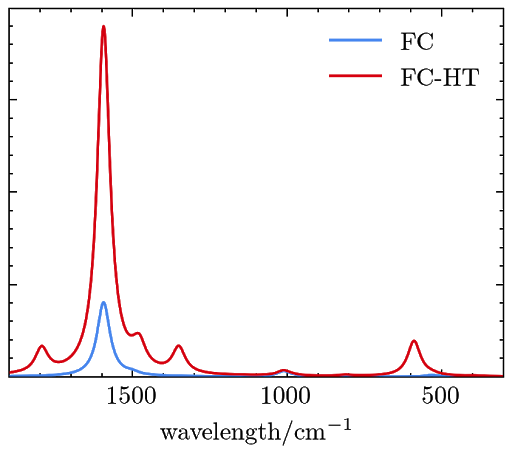
Example 4. Simulating the RRS signals of phenoxyl with TDDFT and the VG model.
Q-Chem Input: ground state (D0) geometry optimization and frequency calculation and excited state force calculation (comments are put after the “!” sign and should be removed in case qchem does not run properly)
$molecule
0 2
C 0.0000000000 1.2267763413 -1.0873977233
C 0.0000000000 0.0003129951 -1.7857718635
C 0.0000000000 -1.2259217607 -1.0872681918
C 0.0000000000 -1.2399944954 0.2921692642
C 0.0000000000 -0.0001222804 1.0534497246
C 0.0000000000 1.2400986319 0.2919975911
H 0.0000000000 2.1644176592 -1.6487443117
H 0.0000000000 -0.0006702414 -2.8784475224
H 0.0000000000 -2.1641202680 -1.6480392688
H 0.0000000000 -2.1702849650 0.8642269804
H 0.0000000000 2.1700059139 0.8643911139
O 0.0000000000 -0.0004975303 2.3044892072
$end
$rem
jobtype opt
method b3lyp
basis def2-SVP
sym_ignore true
$end
@@@
$molecule
read
$end
$rem
jobtype force ! excited state force calculation
method b3lyp
basis def2-SVP
cis_state_deriv 3
cis_singlets true
cis_triplets false
cis_n_roots 10
sym_ignore true
save_vibronic_params true ! save the vibronic parameter for later use
$end
@@@
$molecule
read
$end
$rem
jobtype freq ! ground state frequency calculation
method b3lyp
basis def2-SVP
sym_ignore true
vibronic_spectra 3 ! simulating RRS
$end
$vibronic
model 3 ! using the VG model
temperature 0.
freq_range 1. 4000. 1.
time_range 1. 40000
damping 100.
epsilon 25.
$end
The resulted RRS signals are saved in a file named “rrs_spectra.dat” and can be plotted as
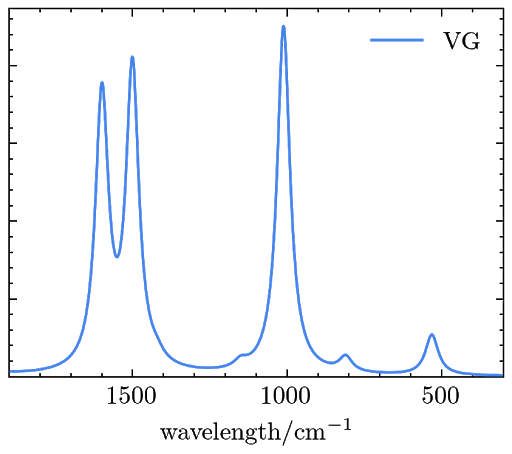
Reference:
[1] Wanzhen Liang et al., J. Phys. Chem. B, 110, 9908 (2006).
[2] Huili Ma, Jie Liu and Wanzhen Liang, J. Chem. Theory Comput., 8, 4474 (2012).
[3] Wanzhen Liang, Huili Ma, Hang Zang and Chuanxiang Ye, Int. J. Quantum Chem., 115, 550 (2015).