Hi, folks. We’re running seemingly straightforward calculations on a small transition metal complex with EOM-SF-CCSD. It is a closed-shell ion, in which the ground state is debatably a singlet or a triplet. It has C2v symmetry.
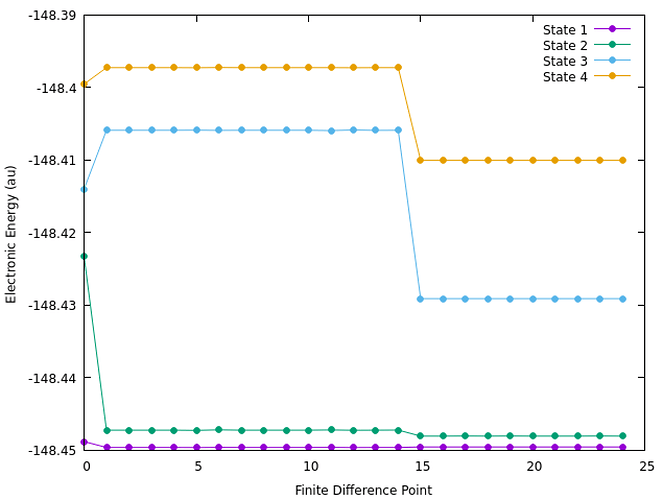
The geometries optimized just fine within each symmetry/state. However, when we run finite-difference frequency jobs, we get odd/large discontinuities and a completely different manifold of states upon displacement. The lowest four states are shown below, with data points corresponding to displacements within the frequency job (point 0 corresponds to equilibrium).
Anybody have a guess what’s happening here?
From my personal experience, two suggestions are offered:
Have you checked the stability of your ground state HF/DFT wave funtion? This is to make sure that your HF/DFT wave function is a local minimum, not a saddle point in the parameter space of MO coefficients.
How many states are you calculating? For example, if I want to use the lowest 4 states, I should compute at least 6~7 states.
Thanks, Jingxiang! Indeed, it turned out to be the SCF that was causing the problems. This particular molecule has several low-lying singlet and triplet states that are nearly degenerate, so it’s kind of an ugly MO problem.
Here’s why the problem wasn’t obvious:
(1) A stability analysis was showing that the SCF was stable, even when lower states were available.
(2) Reading the MOs from the optimization still led to a different SCF solution when running an EOM single-point (for properties/frequencies).
I’ve now been able to carefully craft the correct SCF solution, and all of the discontinuities vanish. The frequencies now nicely match the experiment.
I appreciate the help!
Ryan