T1 Diagnostic for Coupled-Cluster method

Questions
#1

Hello,
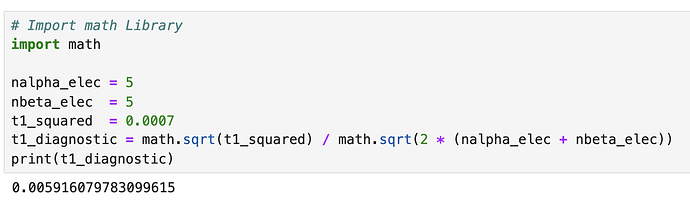
After running CCSD(T) calculation for H2O molecule, I was looking into the output file to find T1 diagnostic value. Can anyone show me where to look? There is only T1^2 value after reporting energies and I don’t know what is referring to.
Thank you for your time.

Input file:

$molecule
0 1
H -2.3527135 2.2827770 0.4401250
O -3.1357501 2.2827770 -0.1660574
H -3.9187867 2.2827770 0.4401250
$end

$rem
jobtype = sp
method = ccsd(t)
basis = def2-SVP
n_frozen_core = fc
ccman2 = true
$end

Output file:

Starting (T) calculation…
Using double precision libpt code
Running restricted (T) code
Using 1 integral batch

(T) calculation completed in 0.01 sec
(T) energy is -0.0031326630

SCF energy = -75.95721338
MP2 energy = -76.16060275
CCSD correlation energy = -0.21302039
CCSD total energy = -76.17023378
CCSD(T) correlation energy = -0.00313266
CCSD(T) total energy = -76.17336644

CCSD T1^2 = 0.0007 T2^2 = 0.0588 Leading amplitudes:

Amplitude Orbitals with energies
0.0097 3 (A1) A → 4 (A1) A
-0.5621 0.1710
0.0097 3 (A1) B → 4 (A1) B
-0.5621 0.1710
0.0075 1 (B1) A → 6 (B1) A
-0.6863 2.4830
0.0075 1 (B1) B → 6 (B1) B
-0.6863 2.4830

Amplitude Orbitals with energies
-0.0512 1 (B2) A 1 (B2) B → 2 (B2) A 2 (B2) B
-0.4957 -0.4957 1.2016 1.2016
0.0512 1 (B2) A 1 (B2) B → 2 (B2) B 2 (B2) A
-0.4957 -0.4957 1.2016 1.2016
0.0512 1 (B2) B 1 (B2) A → 2 (B2) A 2 (B2) B
-0.4957 -0.4957 1.2016 1.2016
-0.0512 1 (B2) B 1 (B2) A → 2 (B2) B 2 (B2) A
-0.4957 -0.4957 1.2016 1.2016

#2

You can calculate the T1 diagnostic by taking the square root of that number and dividing it by $\sqrt{2 * (N_{\alpha} + N_{\beta})$. In Python it might look like

t1_diagnostic = math.sqrt(t1_squared) / math.sqrt(2 * (nalpha_elec + nbeta_elec))
#3

Thank you ericb.
As you helped, I calculated T1 value (T1= 0.00591608) which is really close the value I got it from Molpro software with the same geometry coordinate (T1 diagnostic: 0.00653054).
However, in references, I cannot see multiplier 2 in denominator of T1 formula and I guess this was the reason I got wrong answers.
t1_diagnostic = math.sqrt(t1_squared) / math.sqrt(2 * (nalpha_elec + nbeta_elec))

Thank you again!

#4

Apologies, the factor of two in the denominator is only for a RHF reference. It is not there for UHF; it is related to the number of doubly-occupied orbitals.

#5

Could you please address a follow-up question? Do you include the factor of two in the denominator for a RO-HF reference?

#6

Dear @mitra_rooein ,

May I know which values you have taken for nalpha_elec and nbeta_elkec? I considered your
0.0097 3 (A1) A → 4 (A1) A
-0.5621 0.1710
0.0097 3 (A1) B → 4 (A1) B
-0.5621 0.1710
bold values. Are those correct? If so, my calculated values are as follows: 0.005219. You mentioned 0.00591608! Maybe the values you considered are not correct for me. Please let me know, which values are exact for the nalpha and nbeta electrons. It would be appreciable for your kind answer I am expecting.

Regards
Keshab K. Adhikary

#7

Hello @Keshab_K_Adhikary,
This is the equation in Python provided by @ericb:

Screenshot 2024-03-23 at 7.15.14 PM
Screenshot 2024-03-23 at 7.15.14 PM1976×578 56.9 KB

Note that in Lee and Taylor’s article (1989) for T1 diagnostic, T1=||t1||/(Nelec)^1/2, and they defined Nelec as only the valence electrons.